Climate variability is a determinant within the environmental problems influencing the respiratory syncY_tial virus behavior that cause acute respiratory infections. In spite of the several researches worldwide, predictions of respiratory syncY_tial virus circulation related with climatic conditions are not yet available.

Objective: To propose spatial-temporal models with capacity to predict the respiratory syncY_tial virus behaviorand the areas of major viral activity in the country from climatic conditions.

Methods: An ecological study with prospective analysis of time series combined with spatial statistic was performed. Two indicators were considered: the Respiratory SyncY_tial Virus and the climatic variability described by the Bulto indexes. For the identification of the spatial structure the spatial weight matrix was used, calculated with the spatial weight by distance (with 20 km threshold). Spatial simulation was carried out with Simultaneous Autoregressive models. Concordance among real and predicted values was determined by a concordance index and the Skill factor.

Results: Both temporal and spatial models for prediction of the viral circulation from climatic conditions were proposed using the Bulto complex indexes. Temporal model ability: 0.89012 and Quadratic Mean Error: 7 cases; concordance value between real and predicted Respiratory SyncY_tial Virus activity: 0.9120 in years 2014-2017. Spatial model ability predicts are between 85% and 93%. The models allowed simulating the behavior of the respiratory syncY_tial virus, which is associated with the pattern of climatic variability to generate the prediction maps with viral activity areas.

Conclusions: Models for simulation and prediction of Respiratory SyncY_tial Virus in spatial and temporal scale from the climatic variability were proposed using of the Bulto complex indexes, which allow to alert changes in the viral activity and circulation with three months in advance, according to the response mechanism of their seasonal pattern in connection with the climatic variability identified for Cuba.

Background

The climatic variability, as primary expression of the climate change, is the most significant environmental problem that humanity will face in the neX_t years [1]. It is currently one of the major challenges to the international scientific community, which could be already influencing in the human health, mainly in pathogenic microbes as the Respiratory SyncY_tial Virus (RSV), an important cause of Acute Respiratory Infections (ARI), mostly in developing countries. Children under five are the most affected by severe epidemics of ARI, with eX_tensive damage and even dead in some cases [2,3]. Because of the burden of ARI to the health system, the Ministry of Public Health of Cuba implemented in 2000 an Integral Program for Care and Control of the ARI, establishing the strategy for facing those infections [4]. It was updated in 2013 [5]. Several studies in different regions of the world have analyzed the association between RSV activity and various climatic elements: atmospheric pressure, relative humidity, temperature, rainfall, wind speed and direction, UV radiation, and point of dew [6,7]. In countries with tropical climate, the studies are limited and virus activity has been associated with the rainy season [7]. In Cuba, RSV presents a well-defined seasonal pattern in the rainy period (May-October) with peaks in September-October, the months with the higher humidity, rainfall and contrasts regarding its thermal regimen. Besides, the level of spatial association of those indicators was determined [1]. In the above mentioned paper [1], nonlinear and heterogeneous structure of the virus activity behavior was identified, in which a spatial structure and high heterogeneity predominated, as well as the influence of the climatic variability described according to the Bulto Indexes [8-11]on the seasonal pattern and the spatial distribution of RSV [1], with a cumulative effect. Based on those findings, the present study propose two models which allow simulate the behavior of spatial distribution and temporal variation of the RSV activity associated to the climatic variation as indicators that let to predict the future behavior of the virus.

Materials and Methods

Study design

A prospective study of nonlinear time series combined with spatial statistic was performed.

Setting

Cuba is a mostly tropical country settled in the Caribbean Sea, with a rainy season in summer (Aw, according to Koppen climate classification). The average annual temperature ranges from 24°C till 26°C and higher in the lowlands and on the eastern coast, with temperatures lower than 20°C in the highest parts of mountains. Despite its tropical condition, some seasonal characteristics are present in its thermal regime, with two well-known seasons: summer (rainy season) from May to October, being July and August the warmest months; and winter (less rainy season) from November to April, being January and February the coldest months. The national average rain record is 1335 mm; however, drought events recurrently occur, the duration of which can persist for several years [12].

Participants

A total of 11462 clinical samples of children under five years old with clinical diagnosis of influenza-like illness, severe acute respiratory infection, bronchiolitis and pertussis syndrome were included in the study.

Variables

Clinical: The total of samples processed in the National Reference Laboratory (NRL) and the positive samples of RSV diagnosed for both RSV type A and B, by provinces and month. RSV cases were considered those with symptoms of ARI and a respiratory sample positive to RSV.

Climate: Monthly series of dissolved oxygen density in air (g / m2), maximum and minimum mean air temperatures (ºC), average thermal air oscillation, average relative humidity of air (%), (Mm), mean atmospheric pressure at sea level (hpa), total precipitation (mm) and the number of days with precipitation 0.1 mm.

Data source and measurements

The clinical samples were obtained in the pediatric sentinel hospitals and ambulatory services from all provinces, with a high quality of data obtained by the microbiological sample data collection and transport established in the National Prevention and Control Program of ARI. Samples were sent to the NRL of the Institute of Tropical Medicine “Pedro Kouri”, for diagnosis and surveillance of ARI with possible viral etiology, between January / 2010 and December / 2015. For RSV detectiona Real-Time Polymerase Chain Reaction assay (RT-RCP). The efficient limit of detection for RSV A and B is 10 and 15 genomics copies, respectively. Moreover, the sensitivity and specificity of the multiplex RT-PCR assays for RSV are 100% and 99, 1% was used [13]. As a sentinel surveillance is used in the country for detecting viral circulation, less than 5% of ARI cases are tested, mainly those with Severe Acute Respiratory Infections hospitalized in Intensive Care Units, which allow to know the virus pattern circulation across the territory. The data of the climatic variables were obtained from the climate station network of the Meteorology Institute in the period 1981-2010 for the baseline and 2010-2015 for the current conditions.

Statistical methods

2.6.1. Models of temporal processes: To modeling the effects of climate variability on the patterns of RSV behavior the following dynamic model is proposed [14]:

${{\displaystyle Y}}_t=\frac{\omega (B){{\displaystyle B}}^b}{\delta (B)}{{\displaystyle X}}_t+\frac{\Theta (B)}{\Phi (B)}{{\displaystyle a}}_t+\mu$ (1)

= V (B)

Where,

V (B): Are the weight of the climatic signals on the virus.

ɷ: Is thepolynomialin B.

B: Is theparameter representing the differences between the entrance variables.

X_t: Is the vector containing the values series of the climatic indexes that simulate the climatic variability.

Y_t: Is the vector containing the virus behavior to which the effect of climatic variability is determined.

The models of formula (1) in the literature are named as autoregressive models with distributed lag (ARDL - Autoregressive Distributed Lag Model) [15].

To model the nonlinear part, we will assume that variance changes in time t, which is described in the following expression [16].

${{\displaystyle \sigma }}_t^2=\omega +\alpha {{\displaystyle \epsilon }}_{t-1}^2+\beta {{\displaystyle \sigma }}_{t-1}^2$ (2)

Then we have a model with no constant variance.

The expression (2) can be modified by an exogenous term, if we assume that variance is modulated by an eX_ternal factor. Then, the previous expression transforms in [8-11].

${{\displaystyle \sigma }}_t^2=\omega +\alpha {{\displaystyle \epsilon }}_{t-1}^2+\beta {{\displaystyle \sigma }}_{t-1}^2+\pi {{\displaystyle BI}}_{r,t,c}$ (3)

These models are the named ARMAX [17,18] if the variance is constant; otherwise, it will be an Autoregressive Model with Non Constant Variance (ARCH-Autoregressive Conditionally Heteroscedastic) with exogenous variable [18]. The inclusion of the BI_r,t,c in the equation 3 constitutes an adaptation to the models of the pollutants impact on metalsstudy [19], now transferred to the studies of impact on health in which the variance change is also incorporated.

Models of spatial processes: Dependence modeling has been a much more studied topic tans other effects of spatial heterogeneity [20], although other authors had already verified the existence of geographical continuity in many phenomena. [21] On the other hand, the study of spatial analysis as an effective technique to know the causes and forms of epidemics and diseases propagation has also been presented [22]. This spatial effect has been studied in other knowledge fields such as the natural resources and environmental [23,24] and the studies on social problems [25,26] in research and development activity (R+D) [23,27]. Models of spatial dependency, also denominated dynamic spatial models, could be defined as those of lineal regression models that consider explicitly the existence of the spatial effects of dependency or autocorrelation. The presence of spatial autocorrelation in a model, limits the traditional use of Ordinary Minimal Square Method (MCO). That’s why it is necessary to perform the estimations by the Maximum Likelihood (ML) method, which has been shown as one of the most used alternatives. At the same time, the analysis of the spatial dependency allows to identify phenomena as eX_ternality or overflow effects in a certain spatial unit [28].

General model of spatial weight: For simulation, the start point is that spatial distribution of virusesis characterized by a strong spatial correlation [1], then the spatial autoregressive model can be used [23,28-30].

$\begin{array}{l}y=\rho Wy+X\beta +u\\ u=\lambda W_{2}u+\epsilon \\ \epsilon ~N(0,\Omega )\end{array}$ (4)

where, y is the vector (nX1) of dependent variable observations, ρ (ro) is the autoregressive coefficient, Wy is the vector of the independent variables weightedby the W matrix of neighbor observations, β is a vector of $kx1$ dimensions of the parameters associated with exogenous variables (it means, without the spatial lag) in the matrix of dimensions $nxk$ (that describe the behavior of the climate variations given the BIs), λ is the coefficient of the spatial autoregressive structure for the μ error and ε is the sample error. The matrix of spatial weights W was calculated using spatial weights by distance (with 20 km threshold), obtaining a bigger spatial autocorrelation. Influence of virus circulation on the bordering areas will depend more from the distance between them than from the areas form and size [30-32]. Selection at the spatial lag or spatial error for each model was based on the Moran’s I value and the Lagrange Multiplier [33], calculated using the pattern fitness residuals according to ordinary least squares. The statistical software, GS-plus 10.0, GeoDa 1.10.08 and SIG, ArcGIS 10.1 were used for the processing and the generation of the different maps at Temporal-Spatialscale.

Prediction of the RSV circulation in Cuba: Even prediction of the epidemic behavior or virus activity in time and start point are necessary, it is also important to know the spatial virus distribution; it means, the areas of higher risk and how it disseminates to the rest of the country. To that, the model proposed in the previous epigraphwas used, and during May 2016 the prediction of RSV circulation in the country began to be used. A map format has been used, which allows predicting the virus circulation in a friendly and very clear way to decision makers. Somehow, it indicates the more dangerous areas with conditions for the appearance of an ARI epidemic attributable to RSV. That result gives answer to the necessities of the early warn systems for health [34].

Measures to quantify the quality of the adjusted models: Currently, there is not any evaluation protocol with specific indicators to this kind of model. So, to validatethe use of simple statistic indicators is preferred. As the Absolute Mean Error (AME), theMean Quadratic Error (MCE) and the bias combined with the concordance index D_i and the Skill Factor [33-37], will be used to measure the precision of simulation and the outputs of prediction. It is understood as precision the level of concordance between a pair of individualsof the predicted values and the observed values in RSV series. We will describe the equations of the two last ones because they are less used.

Concordance index D_i, given the neX_t equation

${{\displaystyle D}}_i=1-\left(\frac{{\displaystyle \sum _{i=1}^n{{\displaystyle ({{\displaystyle P}}_i-{{\displaystyle O}}_i)}}^2}}{{\displaystyle \sum _{i=1}^n{{\displaystyle \left(\left|{{\displaystyle P}}_i-\overline{O}\right|+\left|{{\displaystyle O}}_i-\overline{O}\right|\right)}}^2}}\right)$ (5)

where: 0 ≤ D_i ≤ 1; P: predicted value; O: observed value; and

Ō: mean of the observed values.

If D_i≈ 0, indicates a bad concordance between predicted and observed values

If D_i≈ 1, indicates a good concordance between predicted and observed values

This indexis preferred to correlation r coefficient and the r² determination, since those frequently show deceiving and unreal magnitudes [38].

The Skill Factor was also used, which is given by the following expression

${{\displaystyle \beta }}_i=1-\frac{Var({{\displaystyle P}}_{ob{s}_i}-{{\displaystyle P}}_{es{t}_i})}{Var({{\displaystyle P}}_{ob{s}_i})}$ (6)

Where, I =1, 2, . . . , n, P_obs, are the real observation and P_est are estimated by the prediction model and Var is the variance [39] and its interpretation is similar to the previous index.

Results

Temporal scale

In table 1 the RSV parameter estimations are shown. Both models AR (1)-ARCH (1), with exogenous variable (descriptor indexes of climate variations) are combined. All parameters are significant, with high feasibility and quality obtained by the model to predict the RSV behavior to temporal scale. According to the values of different quality indicators, the model is adequate to simulate and predict the RSV circulation in the country from climatic conditions (Figure 1 and Table 2). Figure 1 shows the concordance level between predicted and real values.

Figure 1: Real and predicted Respiratory SyncY_tial Virus activity using the information of positive samples obtained from the laboratory reports.

Figure 2: Prediction of the Respiratory SyncY_tial Virus (RSV) activity in percent, with the information of positive samples obtained from the laboratory reports of 2017.

Prediction models to spatial scale

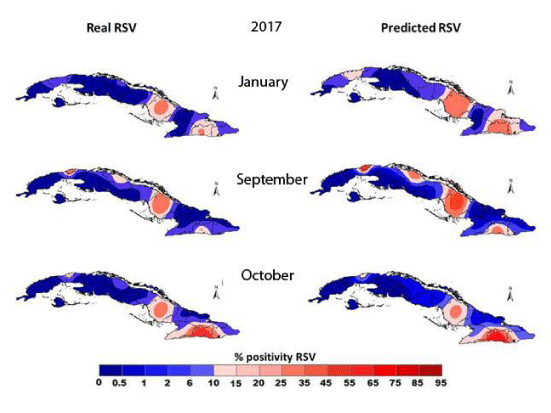
All variables are significant (Table 3) and, as there are not reasons to reject the hypothesis of no spatial autocorrelation of errors, the model results are well specified. Besides, determination coefficient remains below 60%. All their parameters were significant to a confidence level of 95% and 99%. In figure 2, the expected spatial distribution regarding RSV activity in the country is shown., A low circulation in that month is in general observed; although the virus remains circulating in the whole country but not in a same way.

Discussion

Temporal scale

With this model, it is possible to follow the future evolution of the epidemiological patterns in the study region, even with three months in advance, since the variables describing the climatic anomalies present a lag effect or feedback on the pattern of the virus behavior from one to three months [1]. So, climatic situations characterizing RSV variability and change don’t show up in the moment t0, but in the moment t1, t2 and t3. It means, the climate has a cumulative effect on the virus after the climatic anomaly or up to three months later. The results reached with this model, let emitting predictions with effectiveness higher than 80% and with very low errors that can be assumed as they are within the boundary sampling error. This result corroborates the stated by other authors [7,18], who have identified elements of climate (temperature, humidity, cloudy, among other) influencing in the virus behavior and they have tried to formulate models from those elements. The present study differs of those mentionedabove in the way of approaching the climate, because it is not approached by means of isolated elements, but is described with complex indexes [8]. The ARMAX models[18] present two limitations: the climate is not approached in a complex way, but with some elements included; besides, the models present a very strong assumption, when assuming that the information to use should have constant mean and variance. It means absence of Heteroscedasticity, a very typical characteristic of the viruses, which present a marked variability and change in the mean. Those aspects are very well solved in the mentioned research when they transform the information applying finite differences to stabilize the mean and variance, as well as to eliminate the outbreaks or picks, using the ARIMAX or other model [40]. In our proposal, this limitation is overcome considering autoregressive non-linear models with change in variance in an explicit way. This provides a bigger robustness to the results when simulating the viruses circulation and variation as are described in the historical records. That allows us to predict the picks and volatility changes in time; something for which ARIMAX model has not been conceived. Another limitation overcame in this research, is the way in which the influence of the climate on the seasonal pattern of the virus is simulated. This is approachedsince the complexity, using indexes that describe the climatic variations that can alter the virus behavior and circulation, since perceives all the changes of the climatic variables and not each variable separately. In this way, the mechanism of viruses behavior and their association with climate is well understood, because when we are in presence of high humidity and temperatures, this is in general an answer of the variable to a characteristic climatic situation that in general obeys to the presence of a low pressure system, bearing to conversion processes (rainy event). On the other hand, those climatic conditions affect the blood circulation, heart rhY_thm and breathing in the human body, because the heat exchange is intimately linked to the metabolic process, which is regulated by the nervous system. Then, the climatic conditions can favor or not the virus incubation; while in other occasions the organism could become more resistant, favoring or not the condensation and acidification processes in the airways [41]. It was possible to simulatethe behavior of the virus circulation by months and to understand what happens in the months July-August, which is the period when the human being in the study region receives the major effect of the climatic variations and favor the virus circulation. When is conjugated with other conditions, then circulation increases. [16]. As a result of the super saturation and the increase of condensation in upper respiratory airways, destructive additional effects appear, which could have a releasing role in weakening the respiratory airways defense mechanisms and so the increase of the inflammation, dysfunction of the respiratory airways, bronchoconstriction and increase of the snot viscosity in respiratory airways [42,43]. The ARCH component in the model is simulating the variability (volatility) of RSV produced in the previous month and how it influences in the prediction, which is collected in the autoregressive component of information. In this case, it describes the consequence of an outbreak (pick), an intervention, or a climatic anomaly described by the climatic indexes above mentioned on the RSV performance. Therefore, using the previous model, the sign of climatic variability given by the monthly or bimonthly pattern that takes place regularly can be picked up, keeping expressed by the autoregressive component. While, change in variability sign width from a process to another is picked up in change component of variance, which is predicted, allowing preview the neX_t pick. From all the above-mentioned it’s possible to infer that praise worthy models for the simulation and prediction of RSV has been found, which allowed to give an explanation by means of models on mechanisms that they describe. Then the founded models are adequate and offer the possibility of being used for the surveillance of dangerous climatic situations for the human health. However, although the model is appropriate, it presents a positive bias, that is a trend to over estimating the behavior of the virus values, although it is not worrying since the value of the systematic error of the model is framed inside the variance of the original variable. These results confirm the statement [44] that prediction models in which conditional variance is considered, are preferable to the unconditional ones (pure ARMAX) [18]. Since prediction errors are smaller, obtaining better results, then the high level of agreement achieved between the predicted and the real series values of the RSV is evidenced using the models with variance change and incorporation of complex climatic indicators.

Spatial scale

The signs of all coefficients belong together with the relationships found between the climate and VSR behavior, which confirms that positive anomalies in the rainy period (high humidity, high frequency of rainy and cloudy days), conditions which propitiates days with less amount of light-hours that favor the RSV circulation. Spatially, RSV behavior and influence that geographical and climatic conditions have can be explained. The first one when the position in the plan is incorporated and the second one with the incorporation of BI _1,t,pred what allows to explain, by a very simple equation, the relationship (Pred RSV = f) (RSV-1, x,y, BI _1,t,pred). The high significance and quality of achieved adjustments can be observed. Therefore, space distribution of RSV is confirmed as not random, but it is fixed to the physical-geographical characteristics of the setting, the climate variations and the virus characteristics, that find more favorable conditions for their development in some regions more than in others. Then it evidences that simultaneous resolution spatial model (estimation of the coefficients together with the rest of parameters), are appropriate to our objectives and hypothesis, because our purpose was to model the spatial dependence and not filtered, and the autoregressive model has provided us an appropriate simulation of this spatial dependence [1]. The high significance and quality of the achieved adjustments is highlighted. The model’s autoregressive structure represents contagion (rho) between neighbors, where exogenous variables spread between neighboring units, allowing us to understand the dispersion and configuration of RSV and lags (distances), the influence of one region over the neX_t, as well as describing the influence of climate variability as a determinant in each region (the spatial lags and the endogenous variable explain the direct relationship between neighboring units). This confirms the need to understand both spatial and temporal variability in each region in order to understand RSV. Our results confirm that Bulto indexes of climate variability are excellent predictors of RSV spatial distribution that are suitable and consistent as surveillance indicators [11]. The model has high prediction effectiveness as for the months and areas of viral circulation, with agreement levels between 85% and 93%, being the proposed appropriate models for its inclusion in the Cuban Early Warning System. Although models here proposed are more commendable than when considering explicitly the heterogeneity and volatility, when implementing then, limitations and uncertainty should be kept in minds. Statistical models where change in variance, spatial position and distribution in an explicit way are considered, although have had a wide development in the last decades, they still have limitations [16,45]. For instance, in the advance of methods itself (asymmetry modeling) and by geo-referred data readiness (virology and climatic). Besides, when the data of RSV of administrative geographical areas (counties, municipalities, etc.) are taken, sometimes they could not be the most appropriate to describe the studied phenomenon, since it is not necessarily adjusted to the geographical unit. Another uncertainty is that many of the spatial statistic methods have been dedicated to model grouped data (by area or polygon), so there is a risk of ecological fallacy [45]. Hence it is so important to understand the aggregation states, the kind of temporal and spatial variation and why heterogeneity is present, and then defining the interactions matrix and the model. The sensibility analysis of the model was not included in this paper; however, it was performed from the climatic indicator explicit in the model (BI). It was evidenced that changes in the IB don’t alter the order neither the parameters of the model. Since the point of view of prediction, a substantial change is present; for example, if a change in climate is assumed, the prediction changes quickly, showing its sensibility to the climate changes and variations. If the model is run with two scenarios, one of higher climatic variability and trend to be warmer and rainier (more positive values of the index), this generates a different behavior with an increase of the RSV circulation. On the other hand, if conditions trend to more negative BI values (colder and dryer conditions) an RSV decreasing is shown, what corroborates high sensibility to climate changes and variations of RSV. It means, the model keeps its stability regarding the order of the parameters, but changes the predictions output. It is very logical that such changes are show on the RSV series, being then modulated by those changes [1]. They were not explicitly considered other factors in the sensibility analysis because lack of information. But as the proposed models are of conditional variance and changing heterogeneity in the time, which are incorporated in the model formulation, both spatial as temporal; then somehow, if RSV series change, the model reflects the changes in some of the other factors, in an implicit way, because this modulates their behavior.

Conclusions

The suitability and superiority of the Integrated model AR (p)-ARCH (q) on ARMAX model (in which the heterogeneity of the viral circulation is not incorporated) was corroborated. The proposal simulates and predicts in an appropriate way RSV circulation in the country, with a high predictive capacity. The use of spatial weight matrix by distance inside the Spatial Autoregressive (SAR) model was proven as appropriate for simulation of RSV circulation. A space SAR model was proposed, with satisfactory results for identification of more danger areas from climatic conditions for RSV circulation. A model to both temporal and spatial prediction for RSV was developed from climatic conditions. It allows to strengthen health surveillance and to safeguard the population’s life especially of children.

Acknowledgements

Dr. María Guadalupe Guzman (Coordinator of the national project: Impact of climate on Aedes aegypti, dengue, Acute Diarrheal Diseases and Acute Respiratory Infections due to Influenza and SRV in the conteX_t of another environmental, demographic, epidemiological and microbiological variables). This project was partially supported by Ministry of Science, Technology and Environment (grant P211LH007 – 0023) and Ministry of Public Health (grant 131089). The authors would like to thanks the staff members of the of meteorological stations network, those working with the Cuban Meteorology Institute (particularly Dunia Hernandez and María del Carmen Rodriguez) for their assistance in processing climatic data. We also thank the medical and laboratory personnel who provided specimens, in particular those working in diagnosis of RSV (Mayra Mune, Amely Arencibia, Guelsys Gonzalez, Rosmery Roque, Barbara Hernandez).

Authors’ Contributions

All authors participated in conceptualizing the design and coordination, climatic and epidemiological data collection. OP worked in the statistical analysis, the temporal and spatial models and discussion; LY analyzed the data and work in the results interpretation and elaboration of maps; VO, AB and BS worked in the epidemiological and virology analysis; all authors read and approved the final manuscript.

1. Vega YL, Ramirez OV, Herrera BA, Ortiz Bulto PL. Impact of climatic variability in the respiratory syncY_tial virus pattern in children under 5 years-old using the bulto climatic index in Cuba. Int J Virol Infect Dis. 2017; 2: 014-019. https://goo.gl/THzCsi
2. Valdes O, Martinez I, Valdivia A, Cancio R, Savon C, Goyenechea A, et al. Unusual antigenic and genetic characteristics of human respiratory syncY_tial viruses isolated in Cuba. J Virol. 1998; 72: 7589-7592. https://goo.gl/286quV
3. Valdés O, Savon C, Goyenechea A, Palerm L, Gonzalez-Munoz G, Gonzalez-Baez G, et al. Caracterización genética molecular del virus Sincitial respiratorio humano en Cuba. Biotecnología Aplicada. 2005; 22: 149-155. https://goo.gl/u1Mss3
4. MINSAP. Ministry of Public Health. Republic of Cuba. Integral program for care and control of acute respiratory infections. Ministry of Public Health. Republic of Cuba Minsap, Cuba. 2000. https://goo.gl/MVyLUF
5. MINSAP. Ministry of Public Health. Republic of Cuba. Integral program for prevention and control of acute respiratory infections. Minsap ministry of public health. Republic of Cuba, Cuba. 2013. https://goo.gl/DcHQ6x
6. Zhang XL, Shao XJ, Wang J, Guo WL. Temporal characteristics of respiratory syncY_tial virus infection in children and its correlation with climatic factors at a public pediatric hospital in Suzhou. J ClinVirol. 2013; 58: 666-670. https://goo.gl/E3z4e8
7. Paynter S, Yakob L, Simoes EA, Lucero MG, Tallo V, Nohynek H, et al. Using mathematical transmission modeling to investigate drivers of respiratory syncY_tial virus seasonality in children in the Philippines. PLoSOne. 2014; 9: 90094. https://goo.gl/G1jBVK
8. Ortiz PL. Guevara V. Diaz M, Perez. Rapid assessment of methods / Models and human health sector sensitivity to climate change in Cuba. Climate Change: Impacts and Responses. Proceeding of the Conference on National Assessment Results of Climate Change and Health in San Jose, Costa Rica. 1998; 203-22.
9. Ortiz PL, Rivero VA, Perez RA. Modelos Autorregresivos espaciales para la simulacióny pronósticos de enfermedades desde condiciones climáticas. Revista Cubana de meteorología. 2005; 12: 73-92.
10. Ortíz PL, Perez AR, Rivero AV, Perez AC, Ramon CJ, Lecha LE. La Variabilidad y el Cambio Climático en Cuba: Potenciales Impactos en las Salud Humana. Rev Cubana Salud Pública. 2008; 34.
11. Paulo LO, Alina Rivero MS, Yazenia Linares, Alina Pérez MS, Juan R. Vázquez MS.  Spatial models for prediction and early warning of aedes aegypti proliferation from data on climate change and variability in Cuba. MEDICC Review. 2015; 17. https://goo.gl/ZMXGDq
12. Planos E, Vega RyA, Guevara, Editores. Impacto del cambio climático y medidas de adaptación en cuba. Instituto de meteorología, agencia de medio ambiente, ministerio de ciencia, medio ambiente y tecnología. La Habana, Cuba. 2013; 430. https://goo.gl/SeRt2i
13. Arens MQ, Buller RS, Rankin A, Mason S, Whetsell A, Agapov E, et al. Comparison of the Eragen Multi-Code Respiratory Virus Panel with conventional viral testing and real-time multiplex PCR assays for detection of respiratory viruses. J ClinMicrobiol. 2010; 48: 2387-2395. https://goo.gl/dWT9aV
14. Wei, Wiliam WS. Time series analysis (Univariate and Multivariate Methods). New York: Addison -Wesley. 1990. https://goo.gl/1iN41X
15. Greene WH. Econometric Analysis. Published by Pearson. 2011; 1241. https://goo.gl/LuT51X
16. Engle RF. Autoregressive conditional heterocedasticity with estimates of the variance of the U.K. Inflation Econometrical. 1982; 50: 987-1008. https://goo.gl/yUGAmj
17. Ray J, Brownstein J. Nowcasting influenza outbreaks using open-source media reports. SANDIA REPORT.SAND2013-0963. Prepared by Sandia National Laboratories Albuquerque. 2013. https://goo.gl/NXEU8B
18. Chadsuthi S, Iamsirithaworn S, Triampo W, Modchang C. Modeling seasonal influenza transmission and its association with climate factors in thailand using time-series and ARIMAX analyses. Hindawi Publishing Corporation. Computational and Mathematical Methods in Medicine. 2015; 8. https://goo.gl/iNUHYd
19. Enders W. Applied econometrics time series. 1995; 63-128. https://goo.gl/98KzTa
20. Cliff A, Ord JK. Spatial autocorrelation. Pion London. 1973:
21. Cox KR. The voting decision in a spatial conteX_t. Progress in Geography, 1969. First Edition. https://goo.gl/7i1U53
22. Cliff A, Ord JK. Spatial Process. Models and applications. Pion. London. 1981. https://goo.gl/BcMYrk  
23. Anselin L. Spatial Econometrics. In B. Baltagi companion to econometrics. Basil Blackwell, Oxford, UK. 2001.
24. BallerR, Anselin L, Messner S, Hawkins D. Structural covariates of U.S. county homicide rates: incorporating spatial effects. Criminology. 2001. https://goo.gl/Rdmdpg
25. Fischer M, Varga A. Production of knowledge and geographically mediated spillovers from universities. A spatial econometric perspective and evidence from Austria. Proceedings of the 41º ERSA Congress. European Association of Regional Science. 2001. https://goo.gl/X34Z8M
26. Ceccato VR, Haining, Signoreta P. Exploring offence statistics in Stockholm city using spatial analysis tools. Annals of the American Association of Geographers. 2002; 92: 29-51. https://goo.gl/BjK9oC
27. Peralta MA, Rivero VA,  Ortíz BPL. Aplicación del índice climático de Bultó y NDVI captado desde el sensor AVHRR en el estudio del comportamiento delnúmero de Focos de Aedes aegypti en Cuba. Revista de Meteorología Colombiana. 2008; 12: 31-39.
28. Chasco CY. Econometria especial aplicada a la predicción eX_trapolación de datos microterritoriales. Ed. Consejería de Económica e Innovación Tecnológica. 2003.
29. Gaetan C, Guyon X. Spatial statistics and modeling. Springer Science. 2010; 307. https://goo.gl/cDe7hx
30. Anselin L, Rey SJ. Modern spatial econometrics in practice. Press LLC.  2014. https://goo.gl/6BKTV9
31. Moran PA. Notes on continuous stochastic phenomena. Biometrika. 1950; 17-23. https://goo.gl/1KdWvJ
32. Perry J N. Spatial analysis by distance indexes. Journal of Animal ecology. 1995. https://goo.gl/1Kjtvd
33. Bera AK, Yoon MJ. Specification testing with locally misspecified alternatives. Econometric Theory. 1993; 9: 649–658. https://goo.gl/MoHaor
34. Kelly-Hope L, Thomson MC. Seasonal forecasts, climate change, and human health–health and climate.  Adv Glob Change Res. 2008; 30: 31–70. https://goo.gl/TyQZLn
35. Pielke RA. Mesoscale meteorological modeling. 1st Edition Academic Press. 1984; 1-612. https://goo.gl/atiDnm
36. Wackerly, Dennis, Scheaffer, William. Mathematical statistics with applications (7th edition). Belmont, CA, USA: Thomson Higher Education. 2008. https://goo.gl/cUqC29
37. Wilks D. Statistical methods in the atmospheric sciences. 3th ed. 2011; 100. https://goo.gl/iYYD9B
38. Willmott CJ. Some comments on the evaluation of model performance. Bulletin American Meteorological Society. 1982; 63: 1309-1313. https://goo.gl/7QBqVp
39. Livezey RE. The evaluation of forecasts. Analysis of Climate Variability. Springer. 1995; 177-196. https://goo.gl/Qhy9tS
40. Muñoz AG, Thomson MC, Stewart-Ibarra AM, Vecchi GA, Chourio X, Nájera P, et al. Could the recent zika epidemic have been predicted? Front Microbiol. 2017; 8: 1291. https://goo.gl/aFygPy
41. Ishmatov A. On the connection between supersaturation in the upper airways and «humid-rainy» and «cold-dry» seasonal patterns of influenza. 2017. https://goo.gl/E8UX9Q
42. Davis MD, Hunt J. Exhaled breath condensate pH Assays. Immunology and allergy. Immunol Allergy Clin North Am. 2012; 32: 377-386. https://goo.gl/AX3X1h
43. Hoffmeyer F, Berresheim H, Beine A, Sucker K, Bruning T, Bunger J. Methodological implications in pH standardization of exhaled breath condensate. J Breath. 2015; 350-351. https://goo.gl/rY8iPu
44. Tong H. Non-linear time series: A dynamical system approach. Oxford University Press. 1990. https://goo.gl/989Eq8
45. Messner, Anselin L. Spatial analyses of homicide with areal data. Internet. 2002. https://goo.gl/hfWNrL